1 点赞
1 点赞
1 点赞
ThreeJS使用后处理模型变暗处理,使用gammaPass校正
使用EffectComposer添加后处理功能,模型颜色可能会出现异常
2 点赞
1 点赞
2 点赞
1 点赞
0 点赞
patch-package修复npm包的bug
有时我们会遇到node_modules里面安装的npm包与我们的项目不兼容或者有bug,与其给官方提issue并等待官方把npm包修复,还不如我们自己动手,丰衣足食,在可以本地修复的情况下,可以使用patch-package将修改记录下来,并提交到git仓库,这样其他小伙伴也能安装修复代码,达到同步效果。
0 点赞
1 点赞
npm 及 yarn 代理设置及更换为国内下载源
由于有时候网络的原因,会导致 npm 、yarn 下载遇到各种各样的问题。而且我们正好会使用科学上网方法。那么我们就可以为 npm 、yarn 设置代理。让它们通过代理的方式的得到更优的下载网络,从而解决疑难杂症。
 threeJS
threeJS 模型
模型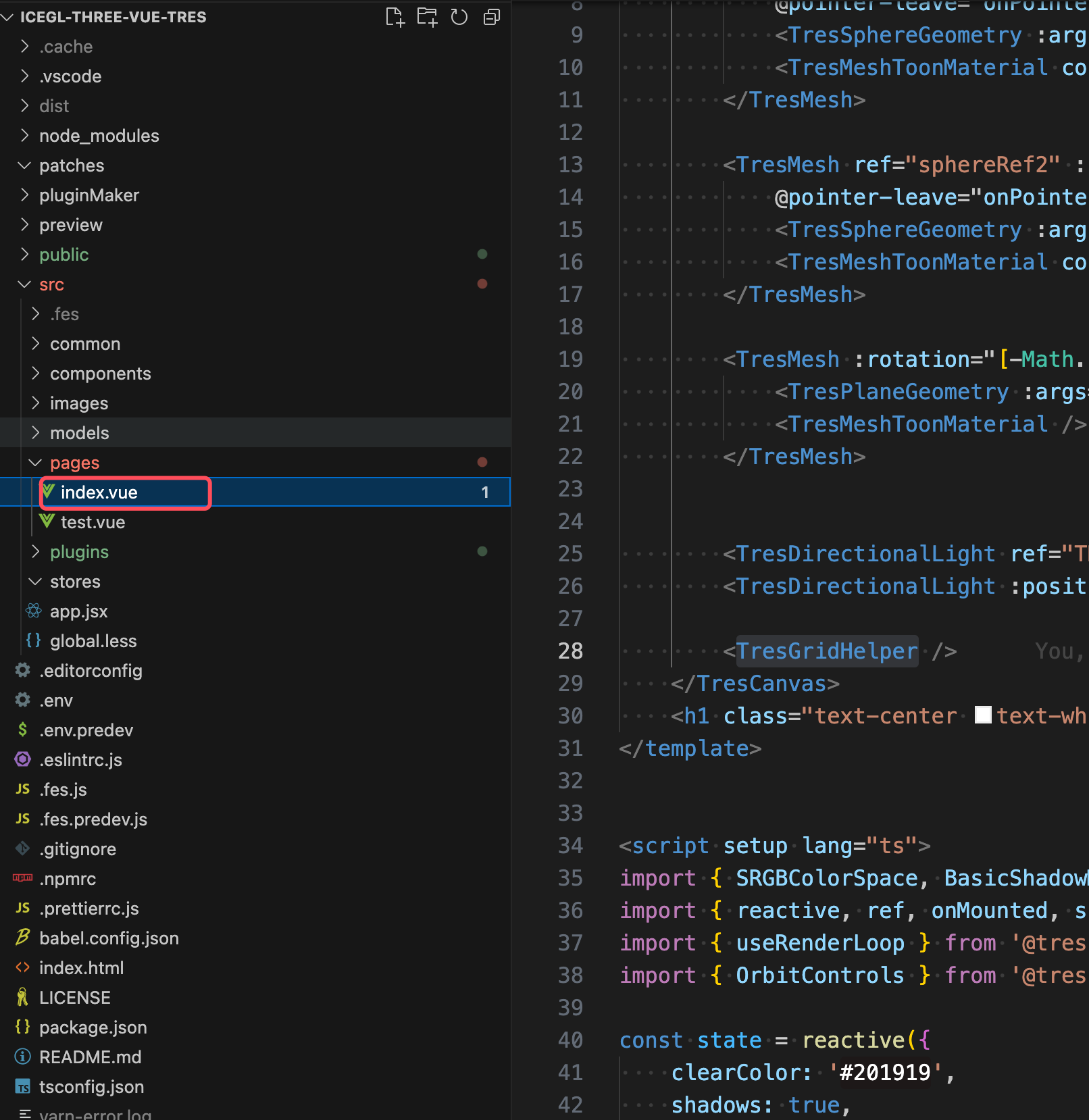




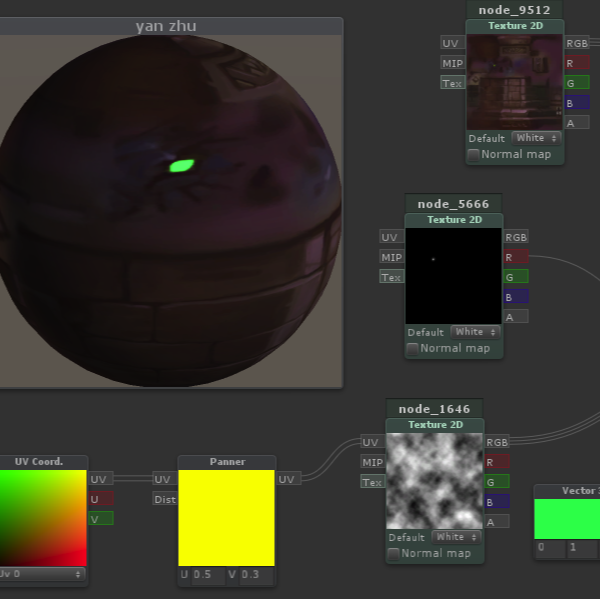 shader
shader WebGL
WebGL cesium
cesium gis
gis glsl
glsl webGPU
webGPU



